堆排序

发表于 | 分类于 | | 阅读次数:
字数统计: 1.4k 字 | 阅读时长 ≈ 5 分钟
堆排序是一种重要数据结构+算法，一般作为优先级队列的底层数据结构，对它的理解有助于我们更好，更快速的对上层工具的使用。

概要

堆排序是一种重要数据结构+算法，一般作为优先级队列的底层数据结构，对它的理解有助于我们更好，更快速的对上层工具的使用。

堆排序原理

堆排序算法介绍

堆是一种重要的数据结构，为一棵完全二叉树, 底层如果用数组存储数据的话，假设某个元素为序号为i(Java数组从0开始,i为0到n-1)。
如果它有左子树，那么左子树的位置是2i+1；
如果有右子树，右子树的位置是2i+2；
如果有父节点，父节点的位置是(n-1)/2取整；
分为最大堆和最小堆，最大堆的任意子树根节点不小于任意子结点，最小堆的根节点不大于任意子结点。
所谓堆排序就是利用堆这种数据结构来对数组排序，我们使用的是最大堆。处理的思想和冒泡排序，选择排序非常的类似，一层层封顶，只是最大元素的选取使用了最大堆。最大堆的最大元素一定在第0位置，构建好堆之后，交换0位置元素与顶即可。堆排序为原位排序(空间小), 且最坏运行时间是O(nlgn)，是渐进最优的比较排序算法。

堆排序的条件

1、是一棵完全二叉树（除了最后一层之外的其他每一层都被完全填充，并且所有结点都保持向左对齐）

2、最大堆要求节点的元素都要不小于其孩子，最小堆要求节点元素都不大于其左右孩子

构造堆的过程（以最大堆为例）

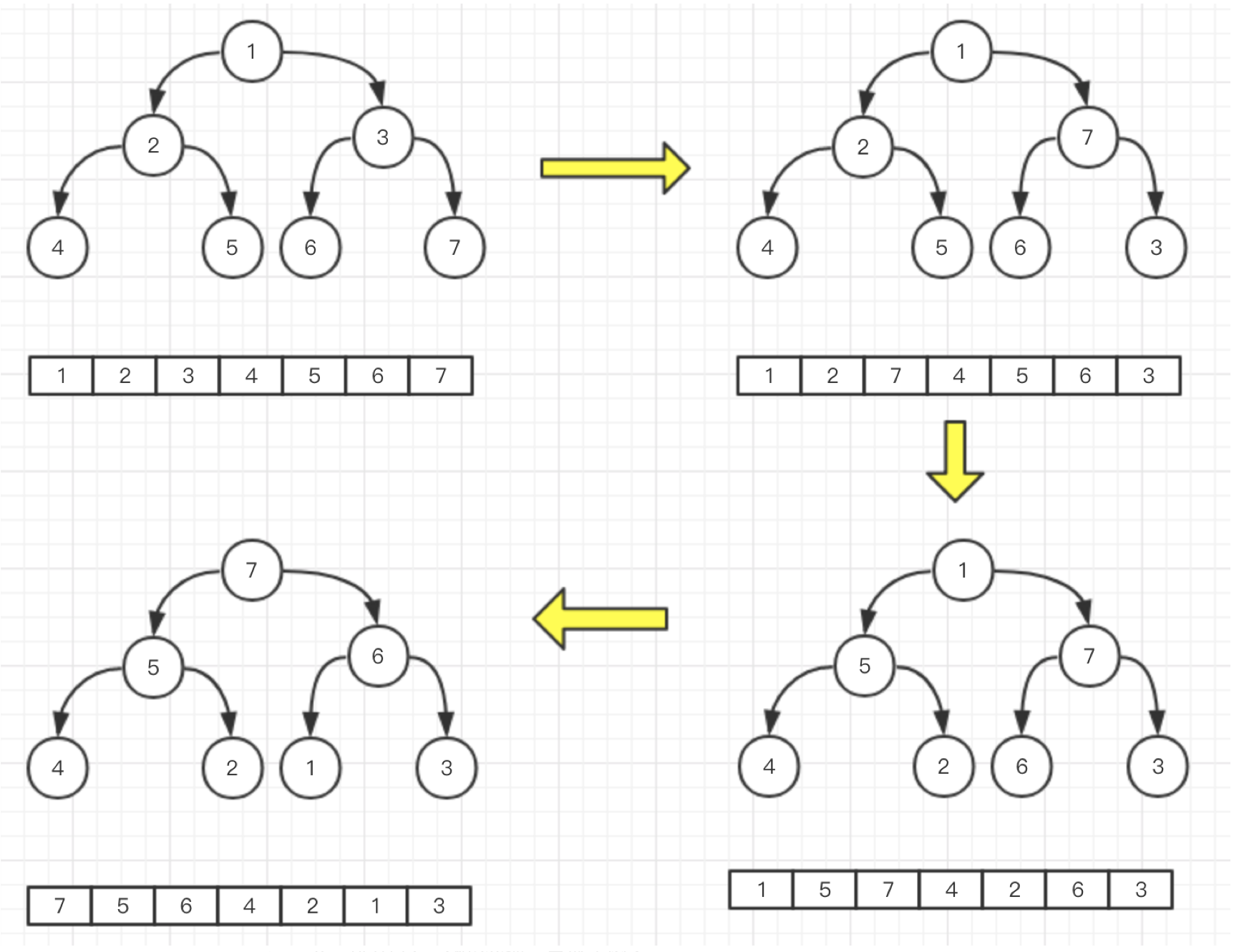
假设初始数组为 [1,2,3,4,5,6,7]
1、从 array.length / 2 开始，即节点4
2、节点4没有子节点，结束
3、到节点3，3和孩子6和7比较，7比较大，和3交换，变成了图2
4、到节点2，2和5交换，变成了图3
5、到节点1，1和7交换后，破坏了原来 7 -> 6, 3 的顺序，需要继续调整，于是1和6交换，变成了图4，结束

堆排序的步骤（以最大堆为例）

1、对数组 n 个元素构建最大堆 （就是上面的过程）
2、将堆顶最大值和数组最后的元素进行替换
3、由于步骤2的的交换可能破环了最大堆的性质，第0个不再是最大元素，就对当前元素进行调整，调整的方法跟上面说的是一样的，最终的结果会得到一个最大堆。

代码及说明

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
public static void heapSort(int[] array) {
        if (array == null || array.length <= 1) {
            return;
        }

        buildMaxHeap(array);

        for (int i = array.length - 1; i >= 1; i--) {
            ArrayUtils.exchangeElements(array, 0, i);
            maxHeap(array, i, 0);
        }
    }

    private static void buildMaxHeap(int[] array) {
        if (array == null || array.length <= 1) {
            return;
        }

        int half = array.length / 2;
        for (int i = half; i >= 0; i--) {
            maxHeap(array, array.length, i);
        }
    }

    private static void maxHeap(int[] array, int heapSize, int index) {
        int left = index * 2 + 1;
        int right = index * 2 + 2;

        int largest = index;
        if (left < heapSize && array[left] > array[index]) {
            largest = left;
        }

        if (right < heapSize && array[right] > array[largest]) {
            largest = right;
        }

        if (index != largest) {
            ArrayUtils.exchangeElements(array, index, largest);
            maxHeap(array, heapSize, largest);
        }
    }

heapSort是入口方法，buildMaxHeap是构建最大堆，maxHeap是每次对节点的调整。
可以看出，我们一开始构建堆，从 array.length / 2 开始，直到第0个，这样就把最大堆构建好了。
maxHeap是核心算法，它的作用是跟两个子节点比较，如果发现有比它大的，就交换，如果发生交换，就从交换的节点继续调整。

总结

用一个数组代表一棵完全二叉树：
左节点在 2*i + 1 的位置
右节点在 2*i + 2 的位置
父节点在（i - 1）/2 的位置

如果要做升序排序则要构造最大堆，因为根节点会输出在数组的最后。

一开始是一个无序的数组，要先构造最大堆，构造最大堆的逻辑就是从 i = （array.length - 1）/ 2 开始，i – ，即从半数开始即可（因为根据完全二叉树的性质，半数之后的都是叶子结点），然后去构造这些子树为最大堆，直到根节点。

当构造好最大堆后，这时根节点肯定为最大值，将根节点与数组最后的数交换，即将最大值输出到最后，这时最大堆被破坏了，需要重新调整，让其符合最大堆的性质，就是从交换后的位置开始，因为如果发生交换了，就说明比较大的节点“上去了”，原来小的父节点“下来了”，但是原来的父节点下来后，是否满足要求呢，要从这个节点继续做调整（整个过程相当于大的节点不停的“浮上去”，小的节点不停的“沉下去”）。

那么完成这一操作后，数组就是按照升序排列。

既然是一个二叉树，堆排序为什么不用链表实现？
其实也是可以的，不过我认为还有几点考虑：
1、链表的结构消耗更多的内存
2、数组可以提供索引来快速检索
3、链表的优势在插入，但堆的数组在插入后的调整也是O(log n)，也不差

参考资料

https://www.cnblogs.com/Java3y/p/8639937.html